
Somebody said infinity?
Can the concept of infinity be properly understood, discussed and compared? This question may sound purely philosophical, but it isn’t in fact. Here I discuss infinity a little.

Cosmology is the scientific field that is devoted to describing the universe and everything at its largest possible scale. How does one do it, and why? In this article, we explore a bit of the ideas behind it.
Over the bare ground in a backyard in the countryside, sits the little person under a clear moonless starry night. Way below the equator line, while looking up, the little man notices a northern concentration of little twinkling stars. “Oh,” thinks the person, “the sky is different everywhere. There’s night and day, a moon that comes and goes. Everything up there… must be hard to see through it all. How complex must it be, to be one mixed and immersed, gazing at the infinity and see its soul…”
Everything…
The way a scientist deals with nature is very reliant on the scale natural to the specific phenomenon. That’s to say: big things are not the same as small things. The most immediate example, for those already initiated, is perhaps the way a physicist chooses to work either with classical physics for big things, where everything can be known with certainty, or quantum physics, in which one deals with the world of the small (thinks electrons, atoms, subatomic particles) where total certainty is impossible, and some certainty of things means ignorance of some others. In some unusual cases, a physicist may work with both classical and quantum physics. Again, a future topic (which I should keep track of, so no empty promises take place).
There is another great example whose scale is absolute: “The everything”, also known as the universe. And I do mean everything. From atoms, to ants, to planets, to galaxies, and further to galaxy clusters and beyond: superclusters and the observable universe. The cosmological scale.
You see, we humans are rather small. So small, in fact, that we have the tendency to undermine how big things can be. Our planet is of course bigger than us, and has all sorts of things on it. Forests, mountains, volcanos, oceans, deserts, islands, rivers etc. For such a diverse list of natural wonders, one thing I’d like to point out they all have in common: they don’t matter in the slightest at the solar system’s scale. And the same could be said about the solar system compared to the Milky Way. Of course, it’s built from billions of stars, among which the Sun is one, but still, its presence on its own is meaningless.
At undergrad school, I attended a lecture from a professor that was rather ordinary. He wasn’t interesting at all, but he did say something that stuck with me: “To develop his theory of gravity, Newton didn’t consider all the wonderful nature: the mountains, the volcanoes, the oceans… everything was just a little dot in the vacuum of space, going around another dot, our Sun.”
This is where I am aiming this article: meaninglessness, scale and the big picture.
In 1915, there was presented to the world a theory of gravity, with the weird name “General relativity” (GE), developed by this famous scientist, Albert Einstein. It is a bit controversial if it was all his idea and doing, but that’s how history sees it. There is a lot of discussion about its philosophical understanding and influences, and also how one can understand it a bit better. But it’s a peanut description (thus, lesser than a nutshell one), so we march forward.
This theory for gravity is rather complicated and to some extent unusual, because gravity would not be a force in itself but a consequence of how the presence of energy (not just mass) affects the space and time (or simply the spacetime) around it. So when an object “falls to the ground,” it’s not exactly falling, it’s just following a very non-trivial “straight line,” and we perceive it as a force, because, in order to avoid this “straight line” movement, we must apply a constant force in the opposite direction on the said object, just to hold it still, much like one would to change the trajectory of a free moving one (remember high school, Newton’s 2nd law!). So, GE is kinda unusual, because all the things that we see when we look up, has some influence in itself but in an indirect manner, namely through its effect on the spacetime around it.
“What is spacetime?” one might ask. It is the entity that is a mix of space and time, and they mix in a way that one can’t have one without the other, let alone describe them separately. There is no universal concept of time either, each one of us experiences it differently. So, this effect gravity has over spacetime, cannot be understood on space and time separately. All these falling objects follow “straight lines in spacetime”, with some “velocity,” and can only be detained by external forces, such as the one you do with your hand to avoid an apple falling to the ground. Cool…? Cool!
Note: I try to avoid the expression “mass curves space and time” because it is inaccurate. Curvature, in the context of GE, is dependent on other notions, such as parallel transport, that itself depend on other definitions that are to some degree arbitrary. Moreover, intrinsic curvature alone can’t determine the shape of most geometrical objects.
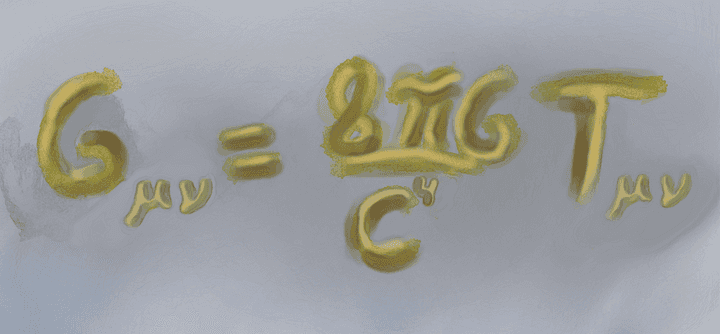
Written down, is Einstein’s field equations for GE. The Greek subscripts are a reminder that there is actually a collection of 16 equations, but only 10 are non-redundant. The “c” is the speed of light, and G, is the gravitational constant, the one proposed by Newton. The left is known as the geometric side, given by the Einstein tensor Gµv,and the right, is the energy part, given by the energy-momentum tensor Tµv. © Hermano Farias.
This theory, GE, is described by 10 equations that work together. The right side ones, which is the geometrical side of things, are derived from 20 independent equations, that in turn are derived from 40 equations that are calculated from 10 quantities (yeah, it sounds ridiculous, but it’s true). These first initial quantities constitute the so-called “metric tensor,” and it’s used to measure distances and time spans, in a mixed fashion, and that is why it is considered the geometrical side.
The right side, as known in the field, is the energy-momentum tensor that encodes the energy that “creates” the geometrical part. So, in a sense, the geometry is given by the energy of things, and the things move in the geometry given by themselves. And that’s it! Rather not straightforward, if I’m honest.
Now we focus on the right side.
So the little man, at the beginning, knows nothing, much less than John Snow. Scale is the thing that makes the starry sky uneven, and unbalanced. But it’s actually not.
Here, we discuss two little concepts, homogeneity and isotropy. And we do it with a grass field. These two qualities are called symmetries, and without them, we would not be able to understand anything, because in physics (and in life) symmetries make things easier.

A grass field (on the left), is usually an example of a homogeneous space. It is basically the same everywhere, as one walks around it. It is also isotropic, since direction is also not important. On the right, we have a field that is not homogeneous, but is isotropic, with respect to the very center of the red leaf circle. © Hermano Farias.
A grass field is very complex and leafy from an ant’s perspective. That’s because an ant is around the scale that makes the grass field complex. There is soil, giant leaves, leaf stems and so on… On the other hand, to a human looking at it, that’s not really the case. If you walk around the grass field, you can’t really say where you started. The same is true if you spin around your axis and stop. You can only tell if you have some reference, such as distant mountains, otherwise grass is grass.
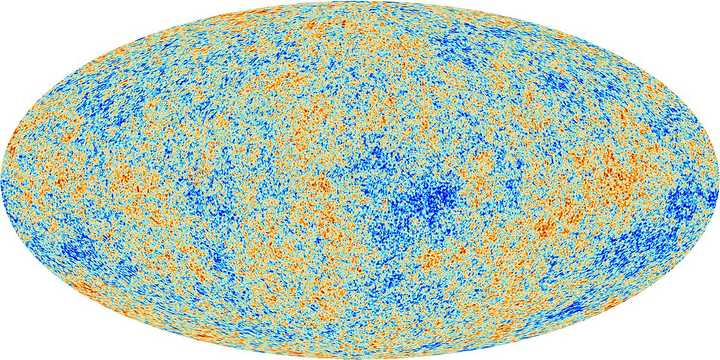
Cosmic background radiation measured as temperature observed 360° around the planet. Source: Wikimedia.
At very large scales, and I mean really large, of about 250 million light-years, we get something similar for the universe, that is, it’s basically the same everywhere, no matter where one looks, and there are no mountains to give you a reference point in the horizon. It may sound a bit strange, but it’s actually true, and there is a lot of evidence out there. One just needs to look deep enough, especially to the past. One of the oldest evidence out there (1)(2), cosmological speaking, is called cosmic background radiation, which can be seen as a snapshot of the universe as a whole, when it was about 300000 years old. No matter the direction one looks, with the right equipment, one sees the same thing, to a surprisingly high degree, varying in a range of only 0.000004 C°.
There is more evidence out there that tells similar stories - our universe is quite the same everywhere, one just needs to look at it in the right scale (3).
This homogeneous and isotropic universe is quite convenient. GE is very fond of symmetries, because they tell a lot about the final form of the metric tensor, which in turn simplify how GE equations should look like.
The assumption of homogeneity, referred to as the cosmological principle, actually reduces all 10 equations to basically one! It is the basis of what is known as homogeneous cosmology. This one equation is for the scale factor, which basically tells the “stretching of everything,” much like an inflating balloon. And it’s growing, in a phenomenon called, appropriately, universe expansion, that is happening to everything, everywhere and all at once. The final form of this parameter depends basically on the ratio of the kind of energy present, radiation kind, like light or microwaves, and dust kind, like in stars (yes, at large scales, stars are dust) and hydrogen clouds.

Possible geometries that depend on how mass is distributed around the cosmos. Here we present the universe in only two dimensions. From left to right, we have positive curvature and closed geometry, negative curvature hyperbolic geometry and flat and open geometry. © Hermano Farias.
Furthermore, homogeneous and isotropic cosmology allows for only three possible geometries: closed, open and flat, or hyperbolic, depending again on the density of energy present in it.
A closed universe is the one that if one chooses a direction, eventually you’re back at the start. A flat universe means that parallel lines remain parallel no matter on what scale. Hyperbolic means no two straight lines are in fact parallel, always drifting apart from one another.
No matter which geometry is correct, one thing that is common among them is: The universe is not static! The scale factor changes with time, no matter how you choose the energy density. Einstein (see the above given link again) had lots of trouble with this fact, to the point of changing his own theory! But that’s another topic.
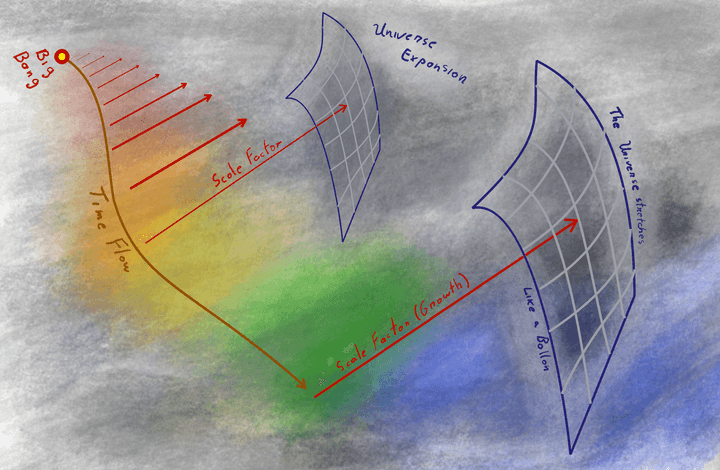
Here is represented the universe expansion through growth of the scale factor, represented by the red arrows. As the factor grows with time, the universe as a whole is stretched. Going back in time, for every known solution for the scale factor, it becomes zero for a given time in the past, a moment known as the big bang, where the entire universe was just a dimensionless dot. © Hermano Farias.
Finally, all these solutions have one final similarity. The universe has a beginning, and in some cases an end. The scale factor is zero at the beginning, and there is no way around it (mostly). This point in time is called the big bang, a singularity, and it’s not necessarily an explosion, but, oh boy, was it hot and unlivable. Again another topic, among many, that this initial introduction creates.
To close this introduction to cosmology, I’d like to summarize: The universe, as far as we know, is very homogeneous. This fact can be used, with Einstein’s General Relativity, to say something about the universe as a whole. And it’s rather simple, in fact one of the simplest forms GE equations can assume. Nevertheless, It’s still very interesting, showing how the universe is at large scales, predicting the big bang and opening up for lots of well posed questions that can be put in a less philosophical fashion, and perhaps be answered.
And don’t feel sad due to your meaninglessness. We, as humans, are the ones making all the questions, and the ones who understand our own meaninglessness. It’s got to be something to be proud of.